目录：

 ●  导读  ●  MNIST 数据集  ●  数据处理  ●  单层隐藏层神经网络的实现  ●  多层隐藏层神经网络的实现

一． 导读

就像我们在学习一门编程语言时总喜欢把“Hello World！”作为入门的示例代码一样，MNIST手写数字识别问题就像是深度学习的“Hello World！”。通过这个例子，我们将了解如何将数据转化为神经网络所需要的数据格式，以及如何使用TensorFlow搭建简单的单层和多层的神经网络。

二． MNIST数据集

MNIST数据集可以从网站http://yann.lecun.com/exdb/mnist/上下载，需要下载的数据集总共有4个文件，其中“train-images-idx3-ubyte.gz”是训练集的图片，总共有60000张，“train-labels-idx1-ubyte.gz”是训练集图片对应的类标（0~9）。“t10k-images-idx3-ubyte.gz”是测试集的图片，总共有10000张，“t10k-labels-idx1-ubyte.gz”是测试集图片对应的类标（0~9）。TensorFlow的示例代码中已经对MNIST数据集的处理进行了封装，但是作为第一个程序，我们希望带着读者从数据处理开始做，数据处理在整个机器学习项目中是很关键的一个环节，因此有必要在第一个项目中就让读者体会到它的重要性。

我们将下载的压缩文件解压后会发现数据都是以二进制文件的形式存储的，以训练集的图像数据为例：

表1 训练集图像数据的文件格式

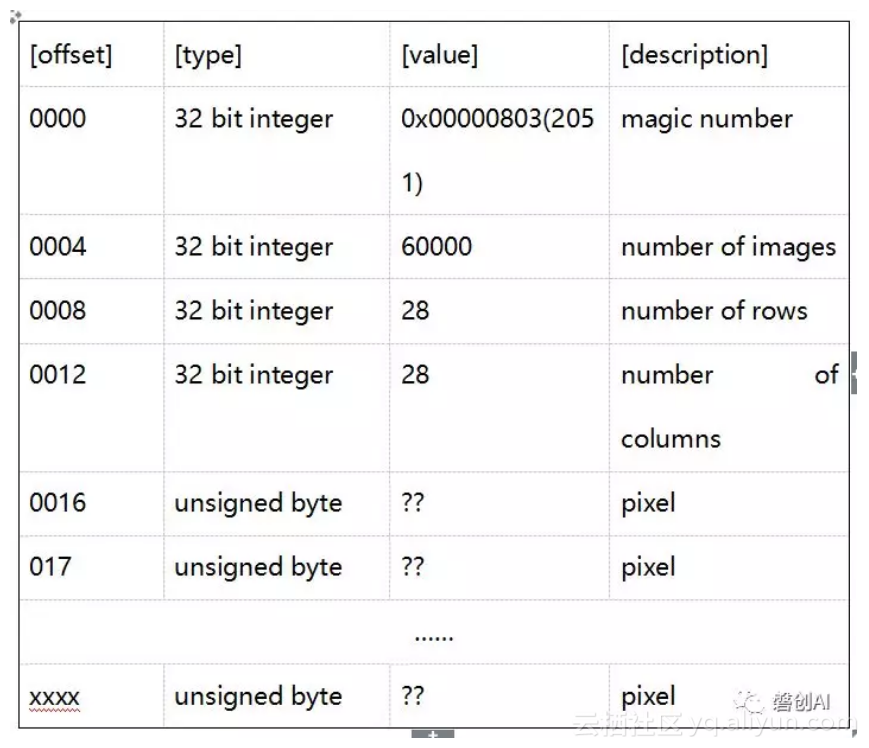
如表1所示，解压后的训练集图像数据“train-images-idx3-ubyte”文件，其前16个字节的内容是文件的基本信息，分别是magic number（又称为幻数，用来标记文件的格式）、图像样本的数量（60000）、每张图像的行数以及每张图像的列数。由于每张图像的大小是28*28，所以我们从编号0016的字节开始，每次读取28*28=784个字节，即读取了一张完整的图像。我们读取的每一个字节代表一个像素，取值范围是[0,255]，像素值越接近0，颜色越接近白色，像素值越接近255，颜色越接近黑色。

训练集类标文件的格式如下：

表2 训练集类标数据的文件格式

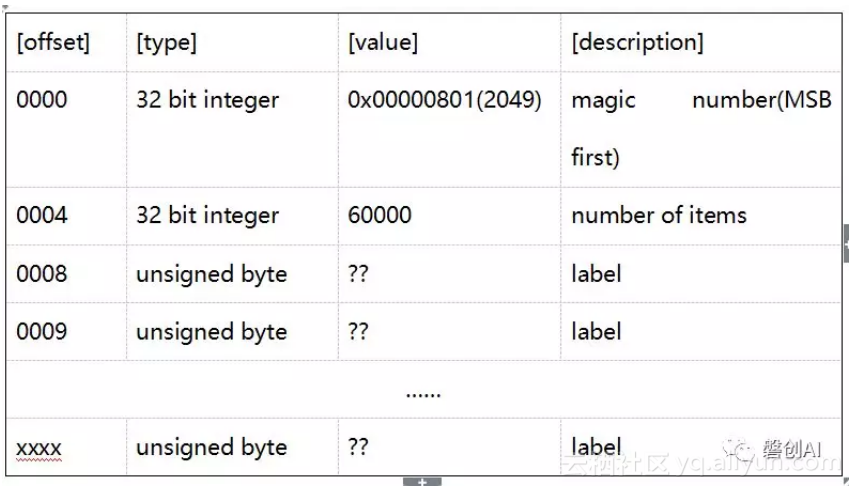
如上表所示，训练集类标数据文件的前8个字节记录了文件的基本信息，包括magic number和类标项的数量（60000）。从编号0008的字节开始，每一个字节就是一个类标，类标的取值范围是[0,9]，类标直接标明了对应的图像样本的真实数值。如图1所示，我们将部分数据进行了可视化。测试集的图像数据和类标数据的文件格式与训练集一样。

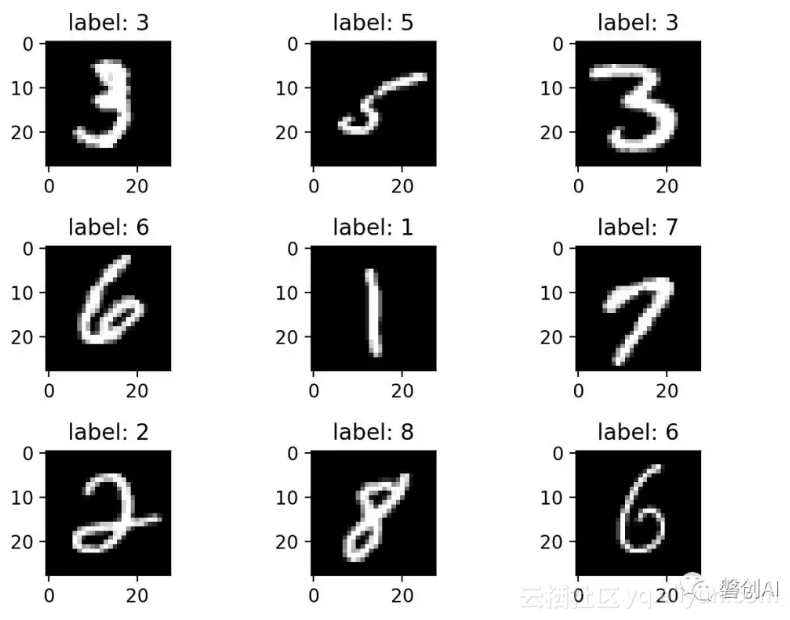
图1 训练集图像数据可视化效果

三． 数据处理

在开始实现神经网络之前，我们要先准备好数据。虽然MNIST数据集本身就已经处理过了，但是我们还是需要做一些封装以及简单的特征工程。我们定义一个MnistData类用来管理数据：

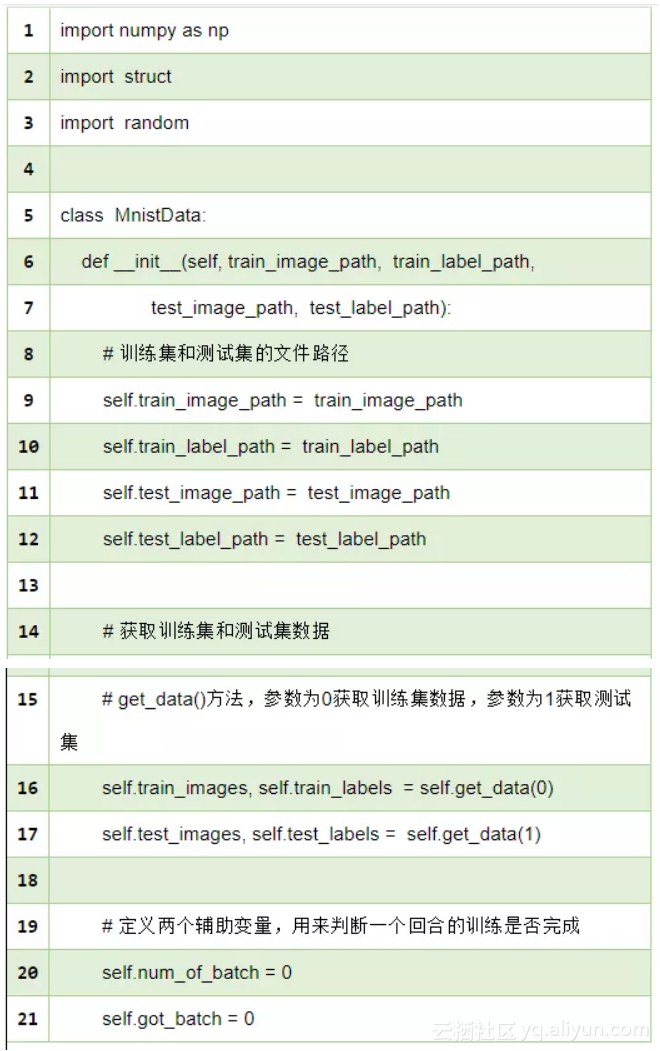
在“__init__”方法中初始化了“MnistData”类相关的一些参数，其中“train_image_path”和“train_label_path”分别是训练集数据和类标的文件路径，“test_image_path”和“test_label_path”分别是测试集数据和类标的文件路径。

接下来我们要实现“MnistData”类的另一个方法“get_data”，该方法实现了Mnist数据集的读取以及数据的预处理。

由于Mnist数据是以二进制文件的形式存储，所以我们需要用到struct模块来处理文件，uppack_from函数用来解包二进制文件，第42行代码中，参数“>IIII”指定读取16个字节的内容，这正好是文件的基本信息部分。其中“>”代表二进制文件是以大端法存储，“IIII”代表四个int类型的长度，这里一个int类型占4个字节。参数“image_file”是尧都区的文件，“image_index”是偏移量。如果要连续的读取文件内容，每读取一部分数据后就要增加相应的偏移量。

第51行代码中，我们对数据进行了归一化处理，关于归一化我们在第一章中有介绍。在后面两节实现神经网络模型的时候，读者可以尝试注释掉归一化的这行代码，比较一下做了归一化和不做归一化，模型的效果有什么差别。

最后，我们要实现一个“get_batch”方法。在训练模型的时候，我们通常会用训练集数据训练多个回合（epoch），每个回合都会用且只用一次训练集中的每一条数据。因为我们使用随机梯度下降的方式来更新参数，所以每个回合中，我们会把训练集数据分为多个批次（batch）送进模型中去训练，每次送进模型的数据量的大小为“batch_size”。因此，我们需要将数据按“batch_size”进行划分。

在第68行代码中，我们使用了“random”模块的“shuffle”方法对数据进行了“洗牌”，即打乱了数据原来的顺序，“shuffle”操作的目的是为了让各类样本数据尽可能混合在一起，从而在模型训练的过程中，各类样本都可以对模型的参数变化产生影响。不过需要记住的是，“shuffle”操作并不总是必须的，而且是否可以使用“shuffle”操作也要看具体的数据来定。

到这里我们已经实现了Mnist数据的读取和预处理，在后面两小节的内容里，我们会分别实现一个单层的神经网络和一个多层的前馈神经网络模型，实现Mnist手写数字的识别问题。

四． 单层隐藏层神经网络的实现

介绍完MNIST数据集之后，我们现在可以开始动手实现一个神经网络来解决手写数字识别的问题了，我们先从一个简单的两层（一层隐藏层）神经网络开始。

本小节所实现的单层神经网络结构如图2所示。每张图片的大小为[28*28]，我们将其转为长度为784的向量作为网络的输入。隐藏层有10个神经元，在这个简单的神经网络中我们没有在隐藏层中使用激活函数。在隐藏层后面我们加了一个Softmax层，用来将隐藏层的输出直接转化为模型的预测结果。

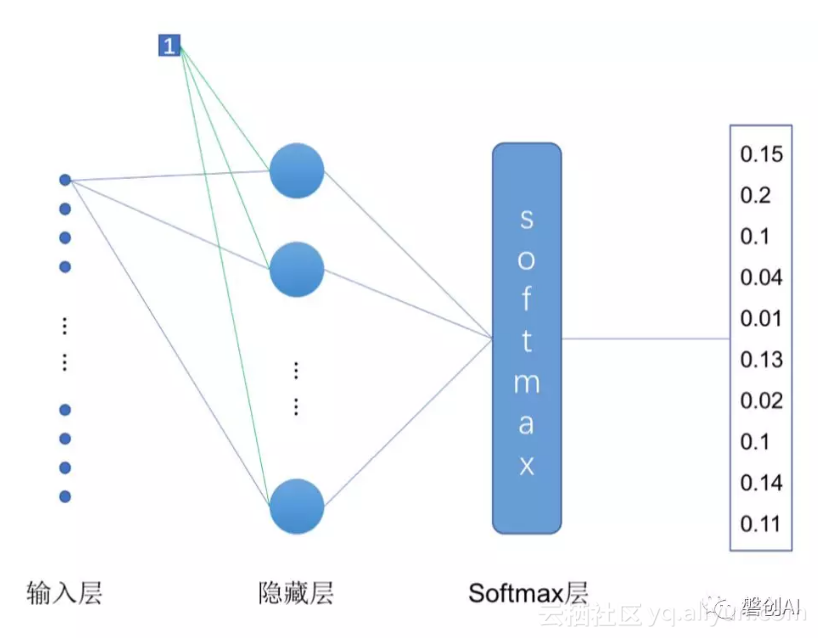
图2 实现Mnist手写数字识别的两层神经网络结构

接下来我们实现具体的代码，首先导入上一小节中我们实现的数据处理的类以及TensorFlow的包：

创建一个Session会话，并定义好相关的变量：

“epochs”是我们想要训练的总轮数，每一轮都会使用训练集的所有数据去训练一遍模型。由于我们使用随机梯度下降方法更新参数，所以不会一次把所有的数据送进模型去训练，而是按批次训练，“batch_size”是我们定义的一个批次的数据量的大小，这里我们设定了100，那么每个“batch”就会送100个样本到模型中去训练，一轮训练的“batch”数等于总的训练集数量除以“batch_size”。“learning_rate”是我们定义的学习率，即模型参数更新的速率。

接下来我们定义模型的参数：

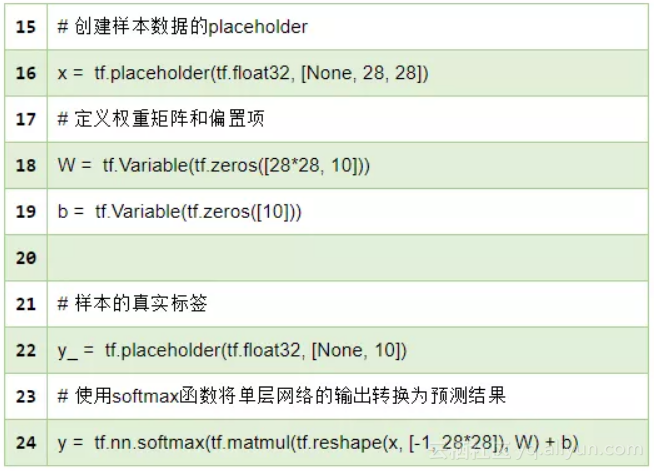
第16行代码定义了输入样本的placeholder，第18和第19行代码定义了该单层神经网络隐藏层的权重矩阵和偏置项。根据图3-16所示的网络结构，输入向量长度为784，隐藏层有10个神经元，因此我们定义权重矩阵的大小为784行10列，偏置项的向量长度为10。在第24行代码中，我们先将输入的样本数据转换为一维的向量，然后进行的运算，计算的结果再经由Softmax计算得到最终的预测结果。

定义完网络的参数后我们还需要定义损失函数和优化器：

第28行我们定义了交叉熵损失函数，关于交叉熵损失函数在本章第三小节中我们已经做了介绍，“”计算的是一个“batch”的训练样本数据的交叉熵，每个样本数据都有一个值，TensorFlow的“reduce_mean”方法将这个“batch”的数据的交叉熵求了平均值，作为这个“batch”最终的交叉熵损失值。

第29和30行代码中，我们定义了一个梯度下降优化器“GradientDescentOptimizer”，并设定了学习率为“learning_rate”以及优化目标为“cross_entropy”。

接下来我们还需要实现模型的评估：

“tf.equal()”方法用于比较两个矩阵或向量相应位置的元素是否相等，相等为“True”，不等为“False”。“tf.cast”用于将“True”和“False”转换为“1”和“0”，“tf.reduce_mean”对转换后的数据求平均值，该值即为模型在测试集上预测结果的准确率。最后，我们实现模型的训练和预测：

因为我们的“batch_size”设置为100，Mnist数据集的训练数据有60000条，因此我们训练600个“batch”正好是一轮。第50行代码中，我们训练完的模型对测试集数据进行了预测，并输出了预测的准确率，结果为0.9228。

五． 多层神经网络的实现

多层神经网络的实现也很简单，我们只需要在上一小节的代码基础上对网络的结构稍作修改即可，我们先来看一下这一小节里要实现的多层（两层隐藏层）神经网络的结构：

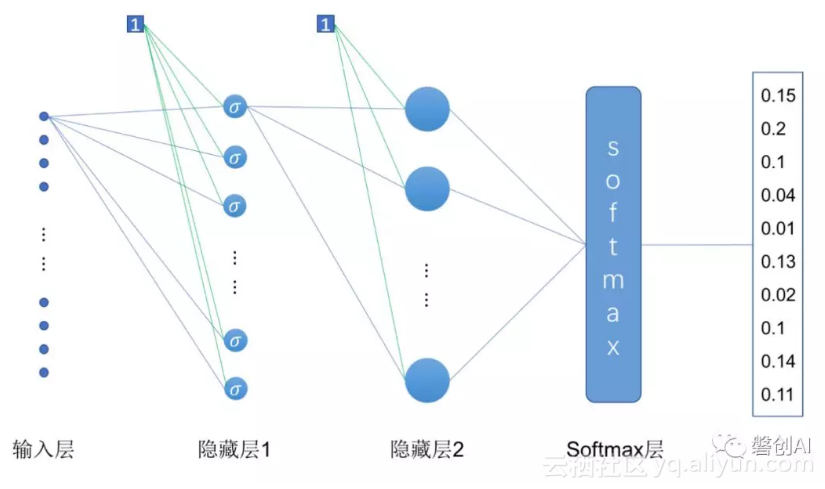
图3 实现Mnist手写数字识别的多层神经网络结构

如上图所示，这里我们增加了一层隐藏层，实现的是一个三层神经网络。与上一小节的两层神经网络不同的是，除了增加了一层隐藏层，在第一层隐藏层中我们还是用了“Sigmoid”激活函数。

实现三层神经网络我们只需要在上一小节的代码基础上对网络的参数做一些修改：

因为网络中有两层隐藏层，所以我们要为每一层隐藏层都定义一个权重矩阵和偏置项，我们设置第一层隐藏层的神经元数量为200，第二次隐藏层的神经元数量为10。这里我们初始化权重矩阵的时候没有像之前那样直接赋值为0，而是使用“tf.truncated_normal”函数为其赋初值，当然全都赋值为0也可以，不过需要训练较多轮，模型的参数才会慢慢接近较优的值。为参数初始化一个非零值，在网络层数较深，模型较复杂的时候，可以加快参数收敛的速度。

定义好模型参数之后，就可以实现网络的具体结构了：

这里具体的计算和上一节内容一样，不过因为有两层隐藏层，因此我们需要将第一层隐藏层的输出再作为第二层隐藏层的输入，并且第一层隐藏层使用了“Sigmoid”激活函数。第二层隐藏层的输出经过“Softmax”层计算后，直接输出预测的结果。最终在测试集上的准确率为0.9664。

原文发布时间为：2018-11-8

本文作者：磐石001

本文来自云栖社区合作伙伴“”，了解相关信息可以关注“”。